高精度运算 高精度加法: int main() { scanf("%s%s",&a1,&b1); if(a1[0] == '0' && b1[0] == '0') { cout << "0"; return 0; } for(int i = 0;i < strlen(a1);++i) a[strlen(a1) - i - 1] = a1[i] - '0'; for(i…
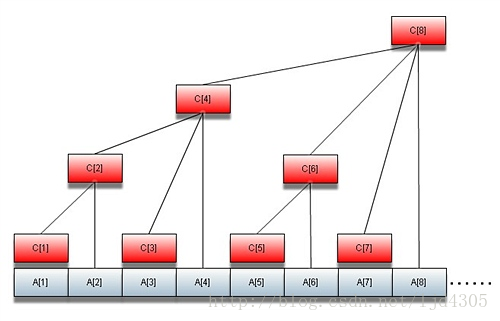
数据结构 树状数组,堆 线段树 单点,区间 动态开结点 并查集 加了路径压缩之后不能随便撤销 使用启发式合并复杂度是 O(n log n),按秩合并是 O(nα(n))。 平衡树 treap 比较好写 splay 比较难写, noip 也不会考这么高级的东西 只能说 (开了 O2 的)set 秒杀一切 dfs 序与树链剖分 非传统方法 点事件 分块 cdq 分治 树状数组 具体思想就是要维护一个序列 a 的前缀和,我们可以维护一个辅助序列 s,使得 si = ∑j2(i-lowbit(i);i] aj,然后我们发…
模板 #define lowbit(x) x & -x //1D void add(int x,int t) { while(x <= n) { v[x] += t; x += lowbit(x); } } int query(int x) { int res = 0; while(x) { res += v[x]; x -= lowbit(x); } return res; } //2D n * m void add(int x,int y,int t) { while(x <= n) { f…
简介 ST表用于区间RMQ问题,它可以做到O(nlogn)预处理,O(1)查询最值。相比线段树,更加有利于静态数据的最值问题。主要是利用倍增的思想。 洛谷:P3865 模板 #include <cstdio> #include <cstring> #include <cstdlib> #include <cmath> #include <algorithm> #include <iostream> #include <vector>…
问题模型 现在有一个这样的问题:有一个数组a,,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和。 这个问题很常见,首先分析下朴素做法的时间复杂度,修改是O(1)的时间复杂度,而查询的话是O(n)的复杂度,总体时间复杂度为O(qn) 可能你会想到前缀和来优化这个查询,我们也来分析下,查询的话是O(1)的复杂度,而修改的时候修改一个点,那么在之后的所有前缀和都要更新,所以修改的时间复杂度是O(n),总体时间复杂度还是O(qn)。 可以发现,两种做法中,要么查询是O(…