问题模型
现在有一个这样的问题:有一个数组a,,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和。
这个问题很常见,首先分析下朴素做法的时间复杂度,修改是O(1)的时间复杂度,而查询的话是O(n)的复杂度,总体时间复杂度为O(qn)
可能你会想到前缀和来优化这个查询,我们也来分析下,查询的话是O(1)的复杂度,而修改的时候修改一个点,那么在之后的所有前缀和都要更新,所以修改的时间复杂度是O(n),总体时间复杂度还是O(qn)。
可以发现,两种做法中,要么查询是O(1),修改是O(n);要么修改是O(1),查询是O(n)。那么就有没有一种做法可以综合一下这两种朴素做法,然后整体时间复杂度可以降一个数量级呢?有的,对,就是树状数组。
lowbit函数
int lobit(int k) {
return k & (-k);
}
lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1
树状数组
这是树状数组的模型
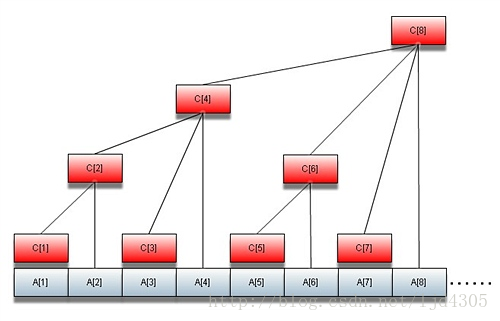
可以看出
C1 = A1 C2 = A1+A2 C3 = A3 C4 = A1+A2+A3+A4 C5 = A5 C6 = A5+A6 C7 = A7 C8 = A1+A2+A3+A4+A5+A6+A7+A8
通过lowbit函数来得出k,其中k就是该值从末尾开始0的个数。然后将其得出的结果加上x自身就可以得出当前节点的父亲节点的位置或者是x减去其结果就可以得出上一个父亲节点的位置。
所以他就变成logn的数据结构了
模板
树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例#1:
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
输出样例#1:
14 16
代码
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 500005;
int a[maxn];
int n,m;
int lowbit(int );
void add(int ,int );
int sum(int );
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 1;i <= n;++i) {
int t;
cin >> t;
add(i,t);
}
for(int i = 1;i <= m;++i) {
int t,x,y;
cin >> t >> x >> y;
if(t == 1) add(x,y);
if(t == 2) cout << sum(y) - sum(x-1) << endl;
}
return 0;
}
int lobit(int k) {
return k & (-k);
}
void add(int i,int t) {
while(i <= n) {
a[i] += t;
i += lobit(i);
}
}
int sum(int i) {
int ans = 0;
while(i) {
ans += a[i];
i -= lobit(i);
}
return ans;
}
树状数组 2
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数数加上x
2.求出某一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含2或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x 含义:输出第x个数的值
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例#1:
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4
输出样例#1:
6 10
代码
#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 500005;
int a[maxn];
int n,m;
int low;
int lowbit(int );
void add(int ,int );
int sum(int );
int main() {
ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 1;i <= n;++i) {
int t;
cin >> t;
add(i,t - low);
low = t;
}
for(int i = 1;i <= m;++i) {
int t;
cin >> t;
if(t == 1) {
int x,y,s;
cin >> x >> y >> s;
add(x,s);
add(y + 1,-s);
}
if(t == 2) {
int s;
cin >> s;
cout << sum(s) <<endl;
}
}
return 0;
}
int lobit(int k) {
return k & (-k);
}
void add(int i,int t) {
while(i <= n) {
a[i] += t;
i += lobit(i);
}
}
int sum(int i) {
int ans = 0;
while(i) {
ans += a[i];
i -= lobit(i);
}
return ans;
}
文章评论