逆元 a * b = 1 (mod p) 则a,b互为逆元 费马小定理 a ^(p-1) = 1 (mod p) p 为质数 -> a * a ^(p-2) = 1 (mod p) 于是 a和a ^(p-2) 互为逆元 欧拉函数 定义:φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) p(1),p(2)…p(n)为x的所有质因数 表示 小于x的数中与x互质的数的数目 欧拉公式:a ^ φ(p) =1 (mod p) -&…
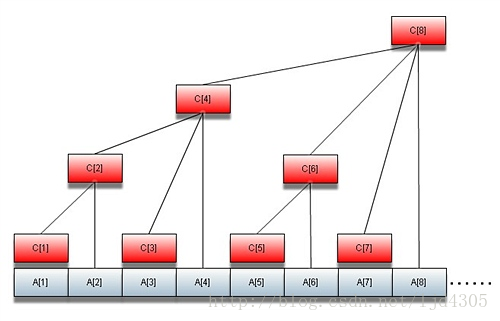
问题模型 现在有一个这样的问题:有一个数组a,,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和。 这个问题很常见,首先分析下朴素做法的时间复杂度,修改是O(1)的时间复杂度,而查询的话是O(n)的复杂度,总体时间复杂度为O(qn) 可能你会想到前缀和来优化这个查询,我们也来分析下,查询的话是O(1)的复杂度,而修改的时候修改一个点,那么在之后的所有前缀和都要更新,所以修改的时间复杂度是O(n),总体时间复杂度还是O(qn)。 可以发现,两种做法中,要么查询是O(…
性质 并查集算法(union_find sets)支持分割一个集合,求连通子图、求最小生成树(克鲁斯卡尔) 输入输出格式 输入格式: 第一行包含两个整数N、M,表示共有N个元素和M个操作。 接下来M行,每行包含三个整数Zi、Xi、Yi 当Zi=1时,将Xi与Yi所在的集合合并 当Zi=2时,输出Xi与Yi是否在同一集合内,是的话输出Y;否则话输出N 输出格式: 如上,对于每一个Zi=2的操作,都有一行输出,每行包含一个大写字母,为Y或者N 输入输出样例 输入样例#1: 4 7 2 1 2 1 1 2 2 1 2 1…
一、埃拉托斯特尼筛法 基本思想:素数的倍数一定不是素数 实现方法:用一个长度为N+1的数组保存信息(0表示素数,1表示非素数),先假设所有的数都是素数(初始化为0),从第一个素数2开始,把2的倍数都标记为非素数(置为1),一直到大于N;然后进行下一趟,找到2后面的下一个素数3,进行同样的处理,直到最后,数组中依然为0的数即为素数。 说明:整数1特殊处理即可。背过就好了。 时间复杂度O(nlogn) 空间复杂度为O(n) #include <cstdio> #include <iostream>…
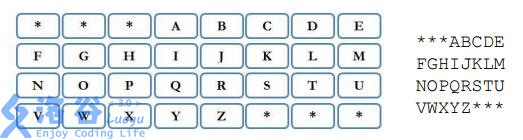
题目描述 C 市火车站最近出现了一种新式自动售票机。买票时,乘客要先在售票机上输入终点名称。一共有N 处:目的地,随着乘客按顺序输入终点名称的每个字母,候选终点站数目会逐渐减少。 在自动售票机屏幕上,有一个4 行8 列的键盘,如下图所示。 在乘客每输入一个字母后,键盘上只有有效字符是可选的(取决于还有哪些候选终点站),其余的字母会被字符'*' 取代。 告诉你N 处目的地的名称,以及乘客已经输入的若干字符,请你输出键盘目前的状态。 输入输出格式 输入格式: 第一行为一个整数N (1≤N ≤50)。接下来N 行,每行一…
题目描述 在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。 每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过 n-1n−1次合并之后, 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。 因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 11 ,并且已知果子的种类 数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少…
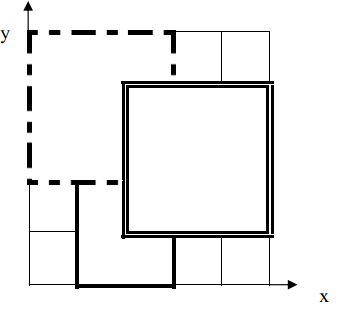
题目描述 为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。一共有 n 张地毯,编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。 地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。 输入输出格式 输入格式: 输入文件名为carpet.in 。 输入共n+2 行。 第一行,一个整数n ,表示总共有 n 张地毯。 接下来的n…
题目背景 本题为提交答案题,您可以写程序或手算在本机上算出答案后,直接提交答案文本,也可提交答案生成程序。 题目描述 将1,2,…,9共9个数分成三组,分别组成三个三位数,且使这三个三位数构成1:2:3的比例,试求出所有满足条件的三个三位数。 输入输出格式 输入格式: 木有输入 输出格式: 若干行,每行3个数字。按照每行第一个数字升序排列。 本人提供的题解 机智的九循环 #include<cstdio> #include<iostream> using namespace std; bool…